1. 
2. Help
3. Log In

Hardy-Weinberg-Gleichgewicht

Die Ableitung der MENDELschen Regeln geht jeweils von zwei Individuen (Eltern) und deren Nachkommenschaft aus. Erbgänge, wie sie bisher beschrieben wurden, können nur unter kontrollierten Bedingungen nachvollzogen werden. Spaltungszahlen wie 3:1 usw. wird man, von bestimmten Fällen abgesehen, in der Natur kaum finden, denn jede Art ist als eine Gruppe von Populationen anzusehen, in der bestimmte Genotypen in ganz bestimmten, aber nur schwer erfaßbaren Anteilen auftreten. Die Häufigkeit eines Allels kann unter Umständen sehr niedrig sein, und Genkombinationen, an denen es beteiligt ist, kommen daher zwangsläufig nur sehr selten vor.

In den Jahren 1908 und 1909 zeigten der Engländer G. H. HARDY und der Stuttgarter Stabsarzt W. WEINBERG unabhängig voneinander, daß die Häufigkeit der Homozygoten und Heterozygoten über Generationen hinweg konstant bleibt, wenn

	die Population sehr groß ist,
	die Individuen sich uneingeschränkt paaren können (vorausgesetzt natürlich, sie gehören unterschiedlichen Geschlechtern an und leben zur gleichen Zeit am gleichen Ort),
	es keine Selektion bestimmter Allele gibt,
	keine Genwanderungen (Genmigrationen) vorkommen und
	keine Erbänderungen (Mutationen) auftreten.

Ihr mathematischer Ansatz ging als HARDY-WEINBERG-Gleichgewicht in die Literatur ein.

Ableitung:

gegeben: ein Allelpaar A und a

angenommen: Die Häufigkeit von A sei p = 0,9 (= 90%), die von a sei q = 0,1 (= 10%)

daraus folgt: p + q = 1

In der Population können daher die Genotypen AA, Aa und aa vorkommen. Die gebildeten Gameten (Eizellen und Pollen) hätten demnach die Konstitution A oder a. Wenn sie zufallsgemäß untereinander gekreuzt werden, müssen wir berücksichtigen, daß A-haltige Gameten mit der Häufigkeit p und a-haltige mit der Häufigkeit q in Erscheinung treten. In der nachfolgenden Generation erscheinen dann die Genotypen

AA = 0,9 x 0,9 = 0,81

Aa = 0,9 x 0,1 = 0,18

aa = 0,1 x 0,1 = 0,01

also: AA = p² Aa + aA = 2pq aa = q²

oder p² + 2 pq + q² = [p + q]² = konstant

In Worte gefaßt: Genhäufigkeiten in Populationen stehen (unter genannten Voraussetzungen) in einem stabilen Gleichgewicht zueinander. Die Zahl der Allele pro Gen in einer Population kann beliebig hoch sein. Das Genom eines Individuums ist daher nur eine zufällige Auswahl (Stichprobe) aus dem gesamten Genpool.

Nach dem HARDY-WEINBERG-Gleichgewicht kann die Häufigkeit der Heterozygoten ermittelt werden. Beim Vorliegen von zwei Allelen kann sie niemals den Wert 0,5 übersteigen.

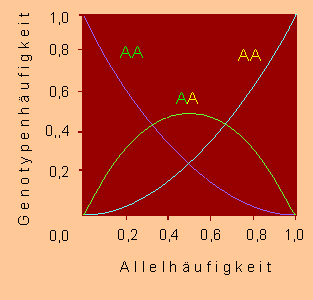
Beziehung zwischen Allel- und Genhäufigkeiten für zwei Allele in einer Population im Hardy-Weinberg-Gleichgewicht (Nach D. S. FALCOMER, 1960)

Ist die Häufigkeit des einen Allels hoch, verschiebt sich das Verhältnis der Genotypen stark in Richtung des entsprechenden homozygoten Genotyps. Weil die genannten Bedingungen in der Regel jedoch nicht realisiert sind, pflanzliche Populationen vielfach sehr klein sind und Selbstbefruchtung nicht selten ist (Populationen bestehen dann genetisch aus nur einem Individuum), entfallen dort die Voraussetzungen für die Gültigkeit des HARDY-WEINBERG-Gleichgewichts. G. MENDEL selbst hat sich 1866 in seiner klassischen Arbeit mit diesem Problem auseinandergesetzt und sich gefragt, wie die Spaltungszahlen in aufeinanderfolgenden Generationen aussehen, wenn die Nachkommen einer jeden Generation stets untereinander weitergekreuzt werden. Durch Extrapolation gelangte er zu folgender Aussage: