Lecture 19Factors determining rates of electron transfer |

(Historical aside- Hook was a contempary or Newton's, jealous of his success, and afraid that he would be scooped on his Law. He hid a preliminary formulation up the chimney in his house,- a coded version of the Latin "ut tensio sic vis" - "as the force, so the tension".)
In Hooks Law, the relation between energy and bond length gives a parabolic curve, and provides the framework for discussion of the dependence of energy on vibrational state, and hence on temperature. As the temperature increased, the increased vibrational energy allows the molecule to "swing" along the parabola, so that it visits the higher energy levels more frequently.
This Hook's Law description is useful in discussion of the energy levels in more complicated molecules. The distance is replaced by a nuclear coordinate, which lumps together all the distances in all the bonds, and a single representative parabola is used to represent the parabolas of all the bonds. This is obviously a gross simplification,- the real picture would require a multidimensional representation,- but it provides a handy frame of reference.
In the diagram below, two different electron transfer reactions are represented, one diabatic, and the other adiabatic. In both cases, the system is represented in two states, that before electron transfer (R the reactant state), and that after electron transfer (P the product state). It is important to realize that these represent two different states of the same system.
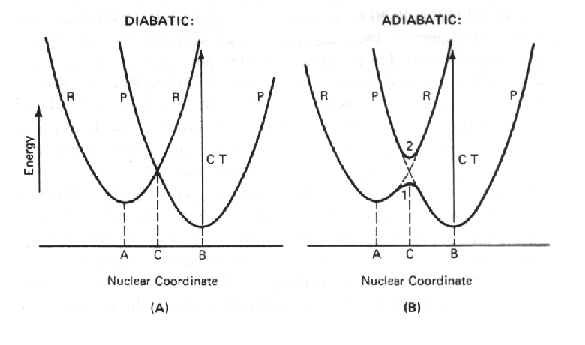
The only place where both conditions are fulfilled is where the nuclear
energy profiles cross (C). The crossing point represents the energy level to which the reactant state must be raises before ptrgressing to the product state. Effectively, this is equivalent to the top of the activation barrier in the Arhenius, Eyring, Randall-Wilkins treatment
The type of process sets a limit to the value of the rate constant:
k in the equation above has a value of 1 if the reaction is adiabatic, less than 1 if diabatic.
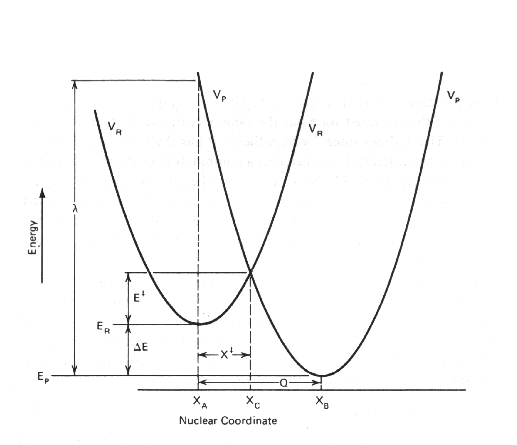
Value for l comes from Hook's Law
l = kHQ2 / 2
From the diagrams, it can be seen l, Eact
and Eo are related, so that:
DEact = (l
+ DEo) / 4l
so that the reorganizational energy depends on the relative positions of the parabolas in both reaction coordinate and energy dimensions.
An important point in this space is the condition under which the Products
parabola intersects the Reactant parabola at the minimum (when Eact is zero). Under these conditions:
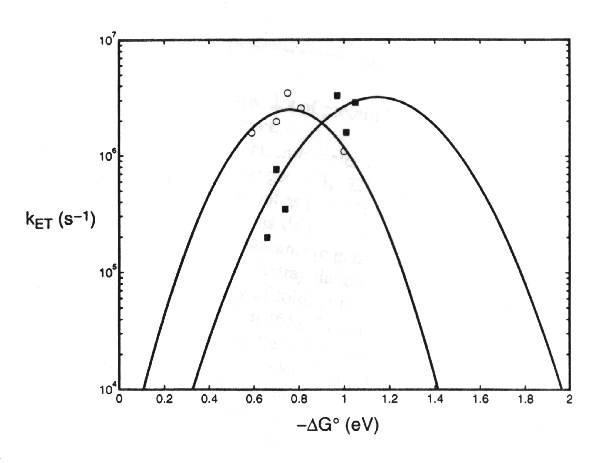
and the reaction proceeds with its maximal rate, with a rate constant (koET) normalized to this condition. Values for (koET) can be found experimentally by measuring the rate constant for a reaction under different conditions, giving different values for DGo. The theoretical curve is shown below:
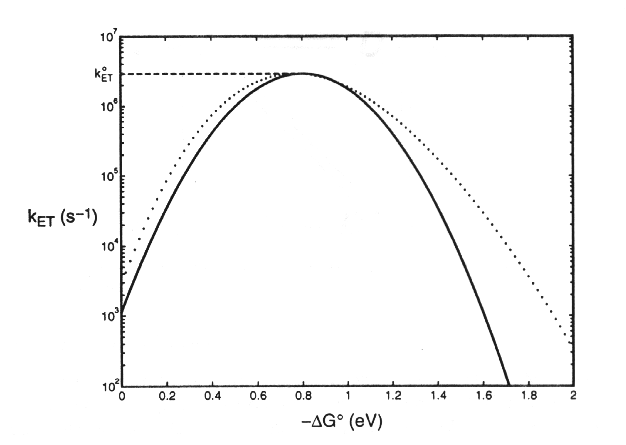
Dutton and colleagues have measured reactions in photochemical reaction centers, and adjusted values for DGo so as to span the range about this value. They have produced an empirical equation (Dutton's Ruler) relating rate to distance:
where R is the edge-to-edge distance in Angstroms, and DG and l are expressed in eV.
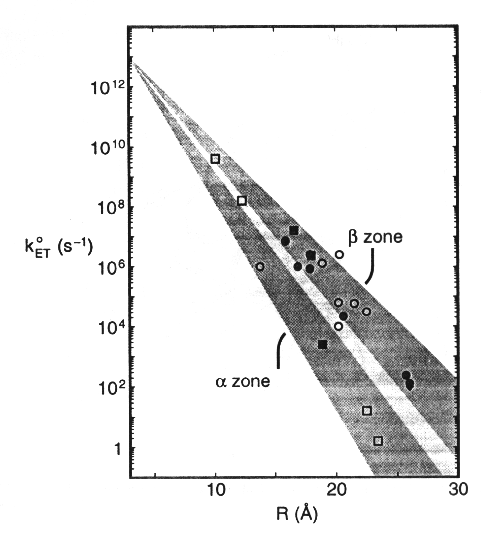
Similar work in Harry Gray's lab has led to some refinement of this picture. They have measured electron transfer rates from ruthenium complexes attached covalently at histines, either native, or positionned by site directed mutagenesis, at different positions to redox proteins with different secondary structures (see example for plastocyanin below).
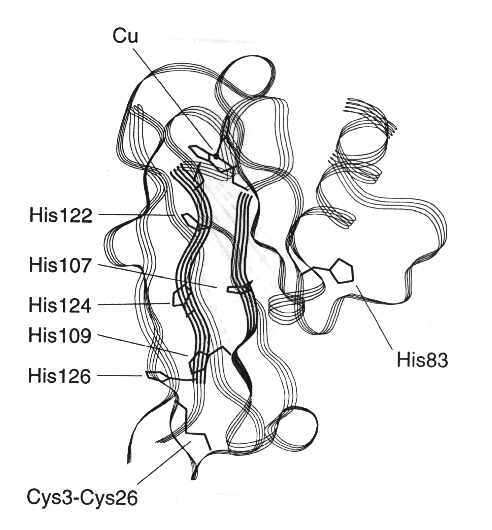
By measuring values for (koET) for different positions in different proteins, the contribution of the secondary structre to the reaction rate could be determined, givinng diifferent slopes for a-helices and b-strands.
(also in more extended form as a book with same title, pp. 207. Cambridge University Press, 1984.)